​
Concentrated Liquidity

With DLMM, LPs can provide liquidity within a specified price range, also known as concentrated liquidity.

This is especially useful for token pairs where trades happen within a tight range, such as USDC/USDT where trades usually happen around $0.99 - $1.01. Often, liquidity outside of this range is untouched and LPs do not earn fees.

By concentrating all liquidity within the price range of $0.99 - $1.01, LPs will be able to optimize their trading fees earned.

All bins except for the active one contain just one type of token (X or Y) because they have been depleted or waiting to be used. Only the active bin earns trading fees.

​
DLMM Bin Structure

​
Bin Price

Liquidity is distributed across discrete bins with a fixed width and fixed price.

Within each bin, liquidity can be exchanged at a fixed price using the formula X+Y=kX + Y = k within each bin. Basically, you add X tokens and take out Y tokens (or vice versa), until there is only one type of token left.

Each bin represents a single price point, and the difference between 2 consecutive bins is the bin step.

Bin steps are calculated based on the basis points set by the pool creator.

Example: Taking SOL/USDC, if the current price is $20 and the bin step is 25 basis points (0.25%), then the consecutive bins would be:

  • Bin 1: $20.00
  • Bin 2: $20.00 × 1.0025 = $20.05
  • Bin 3: $20.05 × 1.0025 = $20.10
  • And so on…

Liquidity pools are identified by their tuple of pooled assets: (Token X, Token Y, Bin Step S)

​
Bin Liquidity

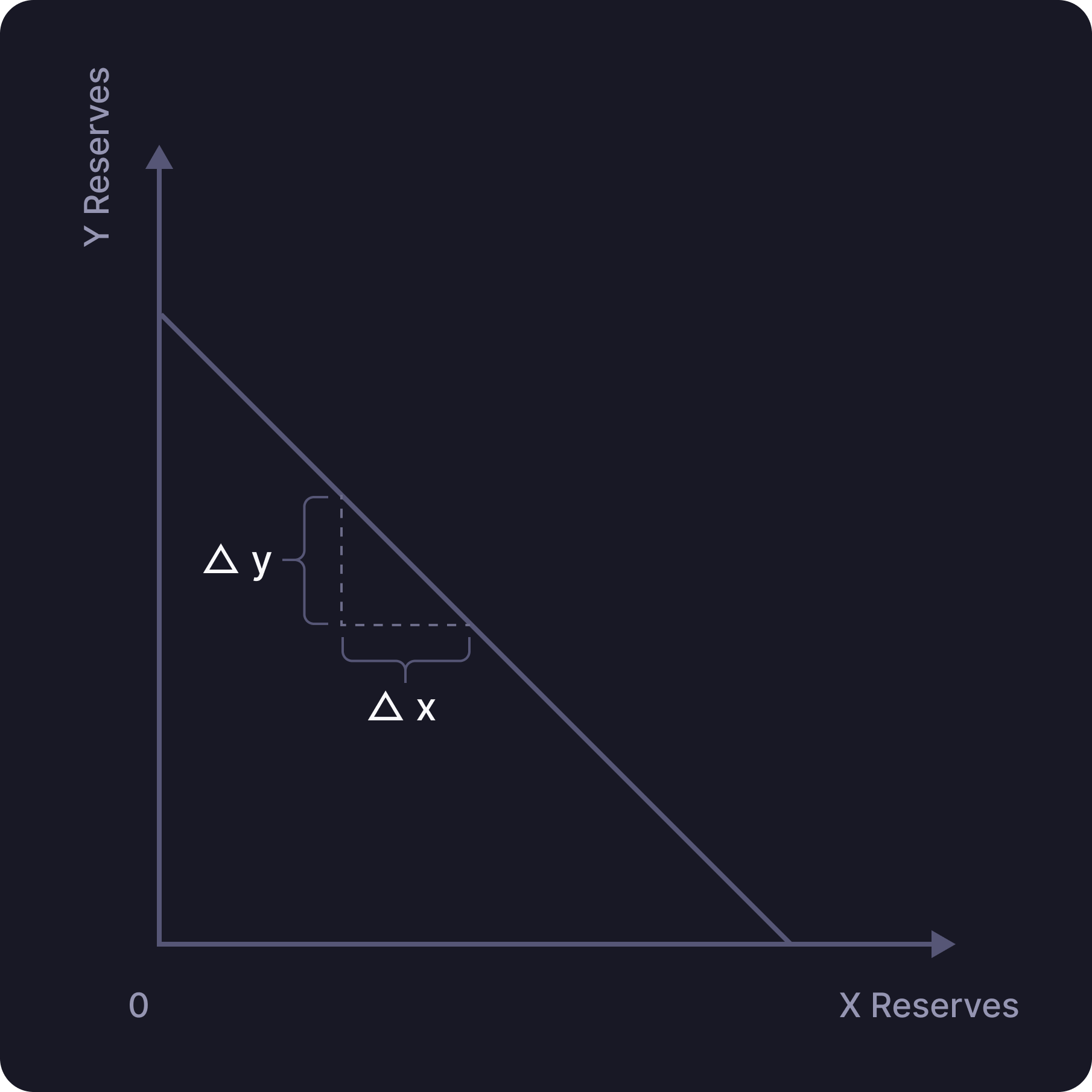
Liquidity in each bin is calculated using the constant sum price variant:

P⋅x+y=LP \cdot x + y = L

Where:

  • x = quantity of token X
  • y = quantity of token Y
  • L = amount of liquidity in the bin
  • P = Δy/Δx = price constant unique to each pool

P is defined as the rate of change of Y reserves per change in X reserves, and represents the price constant unique to each pool.

​
Bin Composition

Key Points:

  • All bins except for the active one contain just one type of token (X or Y) because they have been depleted or are waiting to be used
  • Only the active bin earns trading fees
  • P represents the slope of the line and remains consistently uniform within every bin

In contrast to the constant product formula that you might be familiar with from other AMMs, the price is independent of the reserve amounts of both X and Y. In constant product AMMs, this relationship is calculated by y=P/xy = P/x.

Since the composition of reserves (x and y) are independent of both price and liquidity, an additional variable is used to describe the reserves available in the bin. This variable, composition factor c, is the percentage of bin liquidity composed of token Y:

c=yLc = \frac{y}{L}

From this equation, we can derive x and y:

y=c⋅Ly = c \cdot L x=LP⋅(1−c)x = \frac{L}{P} \cdot (1 - c)

​
Market Aggregation

The constant sum curve intercepts both the x and y axes, meaning that the reserves of X or Y token can be depleted. When this happens, the current price moves to the next bin either on the left or right.

​
Active Price Bin

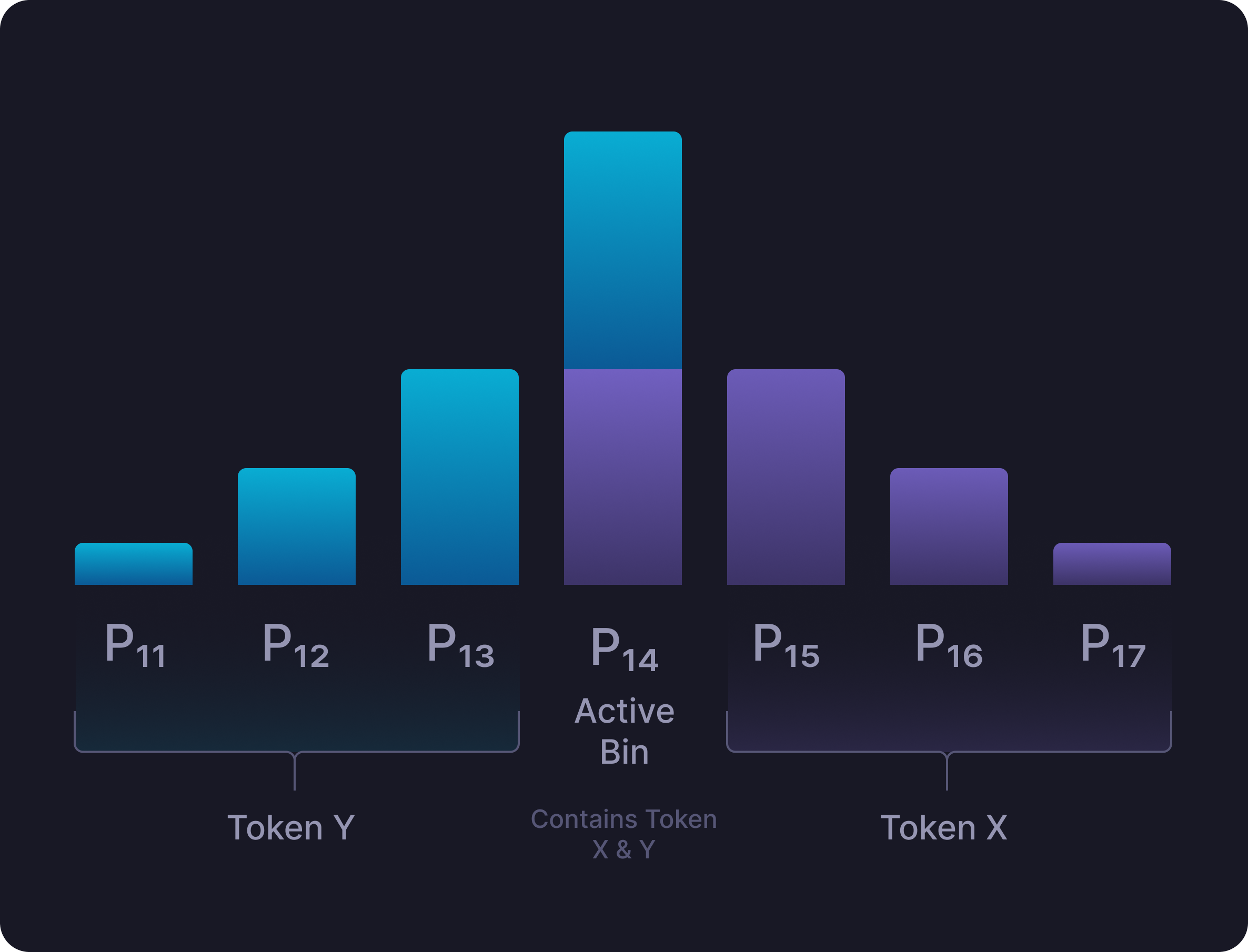
The active price bin is defined as the bin that contains reserves of both X and Y tokens.

Important: There can only be one active bin at any point in time.

  • All bins to the left of the active bin contain only token Y
  • All bins to the right of the active bin contain only token X

​
Practical Example

Consider a SOL/USDC pool where:

  • Asset Y = USDC
  • Asset X = SOL
  • Price P = amount of USDC per SOL

If we define the $100 SOL bin as the active bin:

  • All bins to the left contain only USDC
  • All bins to the right contain only SOL
  • When there is significant demand for SOL, the active bin shifts to the right as the SOL reserves in the $100 bin get exhausted